So recently I’ve been working on more CSS-based transformations and graphics. One of the problems with the current implementation of transform in webkit is that there is no way to individually assign values with JavaScript, making multi-dimensional animations impossible. This is because all of the transformations (like rotateX, translateZ, and scale) are grouped into a single property: -webkit-transform. For example, if you want to rotate 60 degrees in the X and Y axes, you would apply this piece of CSS:
-webkit-transform: rotateX(60deg) rotateY(60deg);

The problem occurs when you try and modify one or both of the values with JavaScript or JQuery. Since JQuery doesn’t support shorthand CSS for the .css() function, there is no way to change either of them without previously knowing the values.

Matrix3D()

The transform property also accepts a 4x4 transformation matrix that is calculated from all seven possible transformations.

matrix3d(0, 1,…15, 16)

Calculating it is pretty math-heavy, so I used a vector math library called Sylvester.js. The function below is heavily based on this tutorial.

The complete function returns a matrix3d value from seven parameters.

function returnMatrix3D(rX, rY, rZ, scale, tX, tY, tZ) {
var deg2rad, scale;
deg2rad = Math.PI / 180; // Degrees to radians constant

var rotationXMatrix, rotationYMatrix, rotationZMatrix, s, scaleMatrix, transformationMatrix, translationMatrix;
rotationXMatrix = $M([
[1, 0, 0, 0],
[0, Math.cos(rX * deg2rad), Math.sin(-rX * deg2rad), 0],
[0, Math.sin(rX * deg2rad), Math.cos(rX * deg2rad), 0],
[0, 0, 0, 1]]);

rotationYMatrix = $M([
[Math.cos(rY * deg2rad), 0, Math.sin(rY * deg2rad), 0],
[0, 1, 0, 0],
[Math.sin(-rY * deg2rad), 0, Math.cos(rY * deg2rad), 0],
[0, 0, 0, 1]]);

rotationZMatrix = $M([
[Math.cos(rZ * deg2rad), Math.sin(-rZ * deg2rad), 0, 0],
[Math.sin(rZ * deg2rad), Math.cos(rZ * deg2rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]);


s = scale;
scaleMatrix = $M([[s, 0, 0, 0], [0, s, 0, 0], [0, 0, s, 0], [0, 0, 0, 1]]);

transformationMatrix = rotationXMatrix.x(rotationYMatrix).x(rotationZMatrix).x(scaleMatrix);
transformationMatrix = transformationMatrix.transpose();
translationMatrix = $M([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [tX, tY, tZ, 1]]);
transformationMatrix = transformationMatrix.x(translationMatrix); // Apply transformation matrix AFTER transposing rotation and scale

s = "matrix3d(";
s += transformationMatrix.e(1, 1).toFixed(5) + "," + transformationMatrix.e(1, 2).toFixed(5) + "," + transformationMatrix.e(1, 3).toFixed(5) + "," + transformationMatrix.e(1, 4).toFixed(5) + ",";
s += transformationMatrix.e(2, 1).toFixed(5) + "," + transformationMatrix.e(2, 2).toFixed(5) + "," + transformationMatrix.e(2, 3).toFixed(5) + "," + transformationMatrix.e(2, 4).toFixed(5) + ",";
s += transformationMatrix.e(3, 1).toFixed(5) + "," + transformationMatrix.e(3, 2).toFixed(5) + "," + transformationMatrix.e(3, 3).toFixed(5) + "," + transformationMatrix.e(3, 4).toFixed(5) + ",";
s += transformationMatrix.e(4, 1).toFixed(5) + "," + transformationMatrix.e(4, 2).toFixed(5) + "," + transformationMatrix.e(4, 3).toFixed(5) + "," + transformationMatrix.e(4, 4).toFixed(5);
s += ")";

return s;
}

Sample Outputs

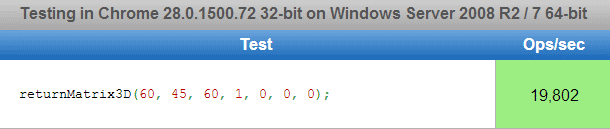
returnMatrix3D(60, 45, 60, 1, 0, 0, 0) - 60deg in X, 45deg in Y, and 60deg in Z. Scale of 1. The value returned is identical to transform: rotateX(60deg) rotateY(45deg) rotateZ(60deg).

matrix3d(0.35355,0.73920,0.57322,0.00000,-0.61237,-0.28033,0.73920,0.00000,0.70711,-0.61237,0.35355,0.00000,0.00000,0.00000,0.00000,1.00000)

Benchmarks

Benchmark ran with jsperf.com. Not sure how accurate this is.